奇函数加偶函数是什么函数？

二者相加一般情况下是非奇非偶函数。设f(x)为偶函数,g(x)是奇函数令f(x)=f(x)+g(x)F(-x)=f(-x)+g(-x)=f(x)-g(x)≠f(x)+g(x)=F（x）也≠-[f(x)+g(x)]=-F(x)即非奇非偶函数。

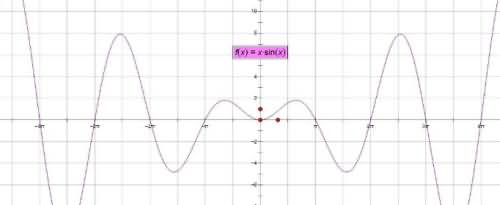
函数（function）在数学中为两不为空集的集合间的一种对应关系：输入值集合中的每项元素皆能对应唯一一项输出值集合中的元素。其定义通常分为传统定义和近代定义，前者从运动变化的观点出发，而后者从集合、映射的观点出发。奇函数加偶函数一般情况下是非奇非偶函数。设f(x)为偶函数,g(x)是奇函数令f(x)=f(x)+g(x)F(-x)=f(-x)+g(-x)=f(x)-g(x)≠f(x)+g(x)=F（x）也≠-[f(x)+g(x)]=-F(x)即非奇非偶函数。

奇函数加偶函数的奇偶性

已知f(x)为奇函数，g(x)为偶函数，且两者的定义域相同，判断f(x)+g(x)的奇偶性。

解：由题意知f(x)=–f(–x)，g(x)=g(–x)，令h(x)=f(x)+g(x)，则h(x)的定义域关于原点对称。

h(–x)=f(–x)+g(–x)，而h(x)不等于h(–x)，–h(–x)=–f(–x)–g(–x)，即h(x)不等于–h(–x)，因此h(x)为非奇非偶函数。

举例说明：f(x)=x，g(x)=x的平方，h(x)=x+x的平方，h(–x)=–x+x的平方，可以看出h(x)为非奇非偶函数。

奇函数减偶函数的奇偶性

已知f(x)为奇函数，g(x)为偶函数，且两者的定义域相同，判断f(x)-g(x)的奇偶性。

解：由题意知f(x)=–f(–x)，g(x)=g(–x)，令h(x)=f(x)-g(x)，则h(x)的定义域关于原点对称。

h(–x)=f(–x)-g(–x)，而h(x)不等于h(–x)，–h(–x)=–f(–x)+g(–x)，即h(x)不等于–h(–x)，因此h(x)为非奇非偶函数。

举例说明：f(x)=x，g(x)=x的平方，h(x)=x-x的平方，h(–x)=–x-x的平方，可以看出h(x)为非奇非偶函数。